В геометрии существует фундаментальное свойство треугольников, касающееся суммы их внутренних углов. Это свойство является базовым для понимания многих геометрических закономерностей.
Содержание
В геометрии существует фундаментальное свойство треугольников, касающееся суммы их внутренних углов. Это свойство является базовым для понимания многих геометрических закономерностей.
Основная теорема о сумме углов треугольника
Сумма внутренних углов любого треугольника всегда равна 180 градусам. Это утверждение справедливо для всех видов треугольников, независимо от их формы и размера.
Доказательство теоремы
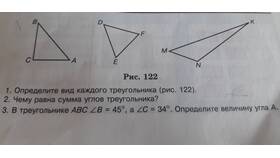
- Рассмотрим произвольный треугольник ABC
- Проведем через вершину B прямую, параллельную стороне AC
- Образовавшиеся углы при вершине B составят развернутый угол (180°)
- Эти углы равны соответствующим углам треугольника как накрест лежащие
- Следовательно, сумма углов A, B и C равна 180°
Примеры для разных типов треугольников
| Тип треугольника | Пример углов | Сумма |
| Остроугольный | 60°, 60°, 60° | 180° |
| Прямоугольный | 90°, 45°, 45° | 180° |
| Тупоугольный | 100°, 40°, 40° | 180° |
| Разносторонний | 70°, 60°, 50° | 180° |
Следствия из теоремы
- В треугольнике не может быть двух прямых или тупых углов
- Внешний угол треугольника равен сумме двух внутренних, не смежных с ним
- Сумма острых углов прямоугольного треугольника равна 90°
- Все углы равностороннего треугольника равны 60°
Применение в задачах
Зная сумму углов треугольника, можно решать различные геометрические задачи:
- Находить неизвестный угол по двум известным
- Доказывать равенство треугольников
- Определять виды треугольников
- Решать задачи на построение
Исключения и особые случаи
В неевклидовой геометрии (например, на сфере) сумма углов треугольника может отличаться от 180°:
- В сферической геометрии сумма больше 180°
- В геометрии Лобачевского сумма меньше 180°
Знание о том, что сумма углов треугольника равна 180 градусам, является краеугольным камнем геометрии и применяется при решении множества задач как в теории, так и на практике.
